Hogyan jelöljük a természetes számok halmazát?
- N
- N0
- Z
- Q
Hogyan nevezzük még a természetes számok halmazát (N)?
- Pozitív egész számok halmaza
- Negatív egész számok halmaza
- Pozitív nemnegatív számok halmaza
- Egész számok halmaza
Hogyan definiáljuk az egész számok halmazát
- Pozitív számok U {0} U negatív számok
- Pozitív számok U negatív számok
- Pozitív számok a nulla nélkül
- Negatív számok a nulla nélkül
Hogyan számoljuk ki két pont közötti távolságot a számegyenesen?
- Megszámoljuk, hogy hány lépésre van egyik szám a másiktól
- Megszámoljuk, hogy hány lépésre van a nagyobb szám a nullától
- Megszámoljuk, hogy hány lépésre van a kisebb szám a nullától
- A nagyobb szám koordinátája lesz a különbség
Minden pozitív számhoz hozzárendelhetünk egy megfelelő negatív számot. Ezeket a számpárokat ____________ nevezzük (helyettesítsd be a helyes választ!
- Ellentett számok
- Abszolút számok
- Pozitív számok
- Negatív számok
Két ellentett szám közül melyik van távolabb a nullától?
- A pozitív szám
- A negatív szám
- Egyforma távolságra vanna
- A nulla
Hogyan jelöljük egy tetszőleges „a” szám ellentett számát
- -a
- +a
- Abszolút érték a
- 0
Egy negatív szám ellentett száma mindig pozitív
- Igaz
- Hamis
Egy szám ellentett számának ellentettje
- Maga az eredeti szám
- Az eredeti szám ellentettje
- Nulla
- Az eredeti szám negatív előjellel
Hogyan nevezzük a számegyenes középpontját
- Origo
- Orion
- Ork
- Ogre
Mit nevezünk egy szám abszolút értékének?
- Egy szám nullától való távolságát
- Egy szám ellentett számát
- Egy szám ellentett számának ellentettjét
- A szám negatív értékét
Két ellentett szám abszolút értéke mindig egyenlő
- Igaz
- Hamis
- Nulla kivételével mindig igaz
Egy pozitív szám abszolút értéke
- Maga a szám
- A szám ellentett értéke
- Nulla
Egy negatív szám abszolút értéke
- A szám ellentett értéke
- Maga a szám
- Nulla
Egy szám abszolút értéke mindig pozitív
- Hamis
- Igaz
Egy szám abszolút értéke mindig nemnegatív
- Igaz
- Hamis
Különböző előjelű számok összeadása
- a nagyobb abszolút értékű szám előjelét lemásoljuk, a számokat kivonjuk
- a nagyobb abszolút értékű szám előjelét lemásoljuk, a számokat összeadjuk
- a kisebb abszolút értékű szám előjelét lemásoljuk, a számokat kivonjuk
- a kisebb abszolút értékű szám előjelét lemásoljuk, a számokat összeadjuk
Két pozitív szám közül melyik a nagyobb
- Amelyik távolabb van a 0-tól
- Amelyik közelebb van a 0-hoz
- Amelyik negatív
- A nulla
Két negatív szám melyik a nagyobb
- Amelyik közelebb van a 0-hoz
- Amelyik távolabb van a 0-tól
- Amelyik pozitív
- A nulla
Két szám közül melyik a nagyobb?
- Amelyik a számegyenesen a másikhoz viszonyítva jobbra helyezkedik el
- Amelyik a számegyenesen a másikhoz viszonyítva balra helyezkedik el
- Amelyik távolabb van a 0-tól
- Amelyik közelebb van a 0-hoz
Melyik állítás az igaz?
Azonos előjelű számok összeadása:
- Előjelet lemásoljuk, számokat összeadjuk
- Nagyobb szám előjelét lemásoljuk, számokat kivonjuk
- Kisebb szám előjelét lemásoljuk, számokat kivonjuk
- Kisebb szám előjelét lemásoljuk, számokat lemásoljuk
Melyik állítás az igaz?
Különböző előjelű számok összeadása:
- Előjelet lemásoljuk, számokat összeadjuk
- Nagyobb abszolút értékű szám előjelét lemásoljuk, számokat kivonjuk
- Kisebb abszolút értékű szám előjelét lemásoljuk, számokat kivonjuk
- Kisebb abszolút értékű szám előjelét lemásoljuk, számokat összeadjuk
Folytasd a mondatot!
Különböző előjelű számok összeadása:
- Nagyobb szám előjelét lemásoljuk, számokat kivonjuk
- Előjelet lemásoljuk, számokat összeadjuk
- Kisebb szám előjelét lemásoljuk, számokat kivonjuk
- Kisebb szám előjelét lemásoljuk, számokat összeadjuk
Folytasd a mondatot!
Azonos előjelű számok összeadása:
- Előjelet lemásoljuk, számokat összeadjuk
- Nagyobb abszolút értékű szám előjelét lemásoljuk, számokat kivonjuk
- Kisebb abszolút értékű szám előjelét lemásoljuk, számokat kivonjuk
- Kisebb abszolút értékű szám előjelét lemásoljuk, számokat lemásoljuk
Több egész szám összeadása esetén mit jelent a csoportosítás?
- Először összeadjuk külön a pozitív, majd külön a negatív számokat, majd a végén a kapott eredményeket
- Először összeadjuk külön a pozitív, majd külön a negatív számokat, majd a végén a kapott eredményeket kivonjuk
- Sorban összeadjuk a számokat
- A feladatokat fiúk-lányok csoportokban oldjuk meg
Hogyan vonunk ki két egész számot?
- Átalakítjuk összeadássá
- Előjelet lemásoljuk, számokat kivonjuk
- Nagyobb szám előjelét lemásoljuk, számokat kivonjuk
- Kisebb szám előjelét lemásoljuk, számokat kivonjuk
Hogyan szabadulunk meg a zárójeltől, ha a zárójel előtt plusz van?
- + jelet elhagyjuk, zárójelet elhagyjuk
- Előjelet megcseréljük, zárójelet elhagyjuk
- Előjel mínusz lesz, zárójelet elhagyjuk
- Előjel plusz lesz, zárójelet elhagyjuk
Hogyan szabadulunk meg a zárójeltől, ha a zárójel előtt mínusz van?
- Előjelet megcseréljük, zárójelet elhagyjuk
- + jelet elhagyjuk, zárójelet elhagyjuk
- Előjel mínusz lesz, zárójelet elhagyjuk
- Előjel plusz lesz, zárójelet elhagyjuk
Több zárójel esetén melyiket számoljuk először?
- A belső zárójelt (legkisebbet)
- A külső zárójelet (legnagyobbat)
- Tetszőlegesen
- Mindig a fekete zárójelet
Mi a sokszögvonal?
- Zárt törött vonal, mely nem metszi önmagát
- Zárt törött vonal
- Zárt vonal, mely nem metszi önmagát
- Vonal, mely metszi önmagát és zárt
Igaz-e a következő állítás?
A háromszögvonal 3 szakaszból álló törött vonal
- Nem
- Igen
- Talán
Miből áll a háromszög?
- Háromszögvonalból
- Háromszögvonalból belső tartomány nélkül
- Belső tartományból
- Háromszögvonalból és belső tartományból
A háromszög belső tartománya
- A háromszög része
- A háromszögvonal része
- A háromszögvonal és a háromszög különbsége
- A háromszögvonalon kívül eső pontok
Melyik állítás az igaz?
- Háromszög = háromszögvonal + belső tartomány
- Háromszögvonal = háromszög + belső tartomány
- belső tartomány = Háromszög + háromszögvonal
- Háromszögvonal = háromszög
Mik azok a kollineáris pontok?
- Olyan pontok, melyek nem tartoznak egy egyeneshez
- Olyan pontok, melyek egy egyeneshez tartoznak
- Olyan pontok, melyek ugyanahhoz a háromszöghöz tartoznak
- Olyan pontok, melyeket azonos betűvel jelölünk
Mit nevezünk nem kollineáris pontoknak?
- Olyan pontok, melyek nem tartoznak egy egyeneshez
- Olyan pontok, melyek egy egyeneshez tartoznak
- Olyan pontok, melyek ugyanahhoz a háromszöghöz tartoznak
- Olyan pontok, melyeket azonos betűvel jelölünk
Fejezd be a mondatot!
A háromszögvonalat alkotó szakaszok a háromszög ...........
- Csúcsai
- Oldalai
- Átlói
- Szögei
Mit nevezünk a háromszög oldalainak?
- A háromszögvonalat alkotó szakaszokat
- A szomszédos oldalak metszéspontjait
- A csúccsal szemközti pontokat
- A csúcsokon áthaladó egyeneseket
Mely oldalakat nevezünk szomszédos oldalaknak
- Melyeknek van közös pontja
- Melyeknek nincs közös pontja
- Melyek metszik egymást két pontban
- Melyek egymással párhuzamosak
A következő állítás: A csúccsal szemközti oldalakhoz nem illeszkedik az adott csúcs
- Igaz
- Hamis
A következő állítás: A csúccsal szemközti oldalakhoz illeszkedik az adott csúcs
- Hamis
- Igaz
Az A csúccsal szemközti oldal:
- BC oldal
- AC oldal
- AB oldal
A B csúccsal szemközti oldal:
- AC oldal
- BC oldal
- AB oldal
A C csúccsal szemközti oldal:
- AB oldal
- AC oldal
- BC oldal
Az A csúccsal szemközti oldal:
- a oldal
- b oldal
- c oldal
A B csúccsal szemközti oldal:
- b oldal
- a oldal
- c oldal
A C csúccsal szemközti oldal:
- a oldal
- b oldal
- c oldal
Az a szög, amelyet a háromszög két oldala határoz meg és a harmadik oldal a szög tartományához tartozik
- a háromszög belső szöge
- a háromszög külső szöge
- a háromszög kerülete
Az a szög, amelyet a háromszög két oldala határoz meg és a harmadik oldal nem tartozik a szög tartományához
- a háromszög külső szöge
- a háromszög belső szöge
- a háromszög kerülete
A háromszög legfontosabb elemei
- Oldalak, csúcsok, szögek
- Név, utca, házszám
- Belső és külső szögek
- Szemközti és szomszédos oldalak
A háromszög szögeit
- Görög ALFABÉTA betűivel jelöljük
- Nagybetűkkel jelöljük
- Kisbetűkkel jelöljük
A háromszög csúcsait
- Nagybetűkkel jelöljük
- Kisbetűkkel jelöljük
- Görög ALFABÉTA betűivel jelöljük
A háromszög oldalait
- Kisbetűkkel jelöljük
- Nagybetűkkel jelöljük
- Görög ALFABÉTA betűivel jelöljük
A háromszög magassága
- A háromszög egyik csúcsa és a szemközti oldal hordozó egyenesére húzott merőleges talppontja közötti szakasz
- A háromszög egyik oldala és a szemközti oldal hordozó egyenesére húzott párhuzamos talppontja közötti szakasz
- A háromszög egyik merőleges és a szomszédos oldal hordozó egyenesére húzott merőleges talppontja közötti szakasz
- A háromszög egyik csúcsa és a vele szomszédos oldal hordozó egyenesére húzott merőleges talppontja közötti szakasz
A háromszög magassága
- Egy szakasz
- A leghosszabb oldalra húzott merőleges
- A háromszög kerülete
- A legrövidebb oldalra húzott merőleges
Mit nevezünk a háromszög magasságpontjának
- A három magasság metszéspontját
- A háromszög középső pontját
- A háromszög magasságának felezőpontját
- A háromszög magasságának egyik csúcsát
A háromszög magassága
- Merőleges az oldalra
- Párhuzamos az oldallal
- Merőleges a háromszög kerületére
- Párhuzamos a háromszög kerületével
A háromszög egyik oldalának hossza kisebb, mint a másik két oldal hosszának összege.
- Igaz
- Hamis
- a+b+c
- (a+b)/2
A háromszög egyik oldalának hossza nagyobb, mint a másik két oldal hosszának különbségének abszolút értéke.
- Igaz
- Hamis
A háromszög egyik oldalának hossza kisebb, mint a másik két oldal hosszának különbségének abszolút értéke.
- Hamis
- Igaz
A háromszög bármelyik oldala a másik két oldal hosszának különbségének abszolút értéke valamint a másik két oldal hosszának összege között van.
- Igaz
- Hamis
-
A háromszög bármelyik oldala a másik két oldal hosszának összegének abszolút értéke valamint a másik két oldal hosszának összege között van.
- Hamis
- Igaz
- Egyenlő szárú négyszög
Az általános háromszög
- Mindegyik oldala különböző
- Mindegyik oldala egyenlő
- Két oldala egyenlő, harmadik különböző
A szabályos háromszög
- Mindegyik oldala egyenlő
- Mindegyik oldala különböző
- Két oldala egyenlő, harmadik különböző
Az egyenlő szárú háromszög
- Két oldala egyenlő, harmadik különböző
- Mindegyik oldala egyenlő
- Mindegyik oldala különböző
Az egyenlő oldalú háromszög
- Mindegyik oldala egyenlő
- Mindegyik oldala különböző
- Két oldala egyenlő, harmadik különböző
A különböző oldalú háromszög
- Mindegyik oldala különböző
- Mindegyik oldala egyenlő
- Két oldala egyenlő, harmadik különböző
Az egyenlő szárú háromszög oldalai
- a – b – b
- a – b – c
- a – a – a
A szabályos háromszög oldalai
- a – a – a
- a – b – b
- a – b – c
Az általános háromszög oldalai
- a – b – c
- a – a – a
- a – b – b
Hogyan hívjuk az egyenlő szárú háromszögnél azt az oldalt, mely különbözik a másik két oldaltól?
- Alap
- Szár
- Kerület
- Különc
Hogyan hívjuk az egyenlő szárú háromszögnél azokat az oldalakat, melyek egyforma hosszúságúak?
- Szár
- Alap
- Kerület
- Különc
Egy belső és egy külső szög összege
- 180°
- 90°
- 360°
- 123°15
Egy külső és egy belső szög összege
- 180°
- 90°
- 360°
- 146°60'
A háromszög belső szögeinek összege
- 180°
- 90°
- 360°
- 45°
A belső szögek összege egy háromszögben mindig
- 180°
- 90°
- 360°
- 45°
A háromszög külső szögeinek összege
- 360°
- 90°
- 180°
- 45°
A külső szögek összege egy háromszögben mindig
- 360°
- 90°
- 180°
- 45°
Milyen összefüggés van a háromszög egy külső és belső szögei között
- A háromszög külső szöge egyenlő a vele nem szomszédos két belső szög összegével
- A háromszög külső szöge egyenlő a vele nem szomszédos két belső szög különbségével
- A háromszög külső szöge egyenlő a vele szomszédos két belső szög összegével
- A háromszög belső szöge egyenlő a vele szomszédos két külső szög összegével
Hogyan szól az általános háromszög kerülete?
- K = a + b + c
- K = a + b + b
- K = a + 2 · b
- K = 3 · a
Hogyan szól a különböző oldalú háromszög kerülete?
- K = a + b + c
- K = a + b + b
- K = a + 2 · b
- K = 3 · a
Hogyan szól a szabályos háromszög kerülete?
- K = 3 · a
- K = a + b + c
- K = a + b + b
- K = a + 2 · b
Hogyan szól az egyenlő oldalú háromszög kerülete?
- K = 3 · a
- K = a + b + c
- K = a + b + b
- K = a + 2 · b
Hogyan szól az egyenlő szárú háromszög kerülete?
- K = a + 2 · b
- K = 3 · a
- K = a + b + c
- K = a+ a + b + b
A képen látható háromszög
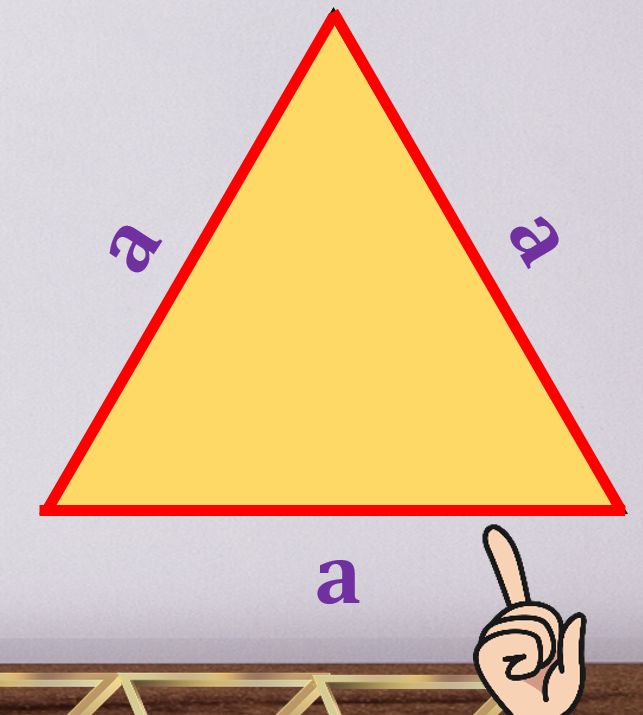
- Egyenlő oldalú háromszög
- Egyenlő szárú háromszög
- Általános háromszög
- Különböző oldalú háromszög
A képen látható háromszög

- Szabályos háromszög
- Egyenlő szárú háromszög
- Általános háromszög
- Különböző oldalú háromszög
A képen látható háromszög
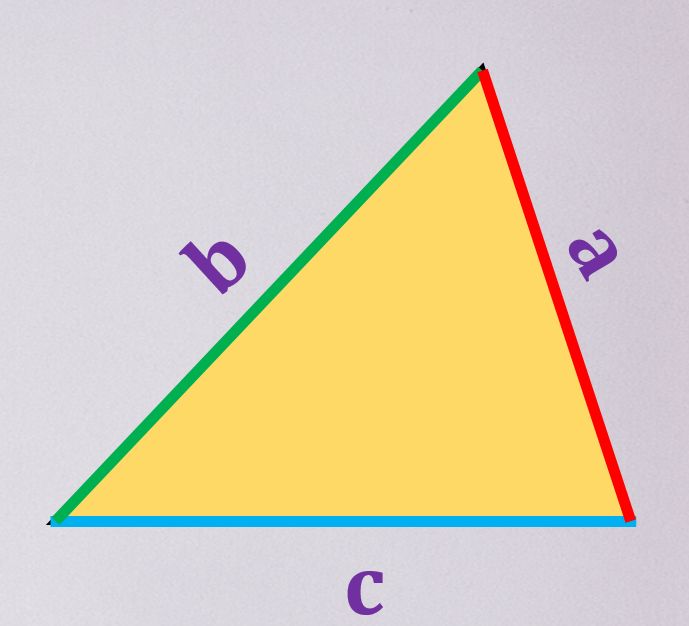
- Általános háromszög
- Szabályos háromszög
- Egyenlő szárú háromszög
- Derékszögű háromszög
A képen látható háromszög

- Különböző oldalú háromszög
- Szabályos háromszög
- Egyenlő szárú háromszög
- Derékszögű háromszög
A képen látható háromszög
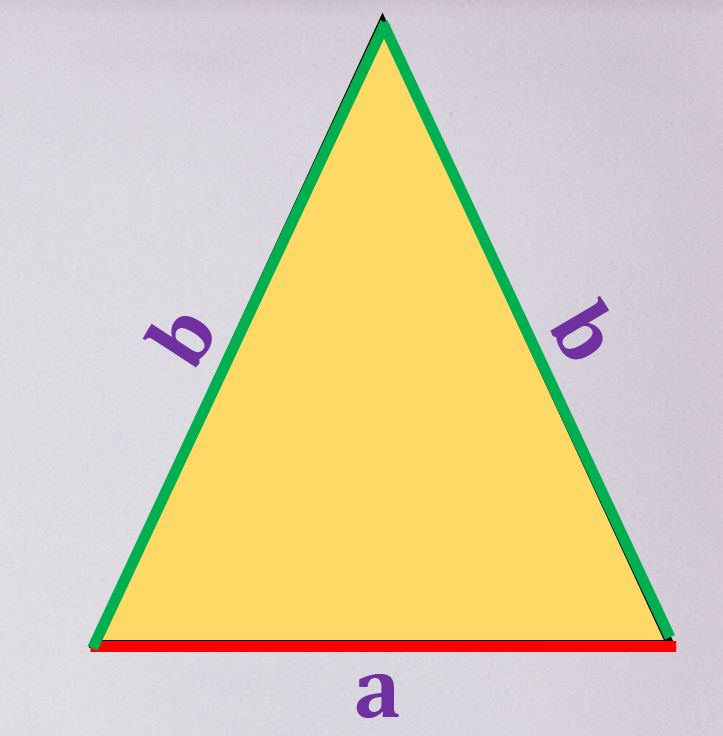
- Egyenlő szárú háromszög
- Szabályos háromszög
- Általános háromszög
- Különböző oldalú háromszög
Mely háromszögnek a kerületét számoljuk a következő képlettel: K = a + 2 · b
- Egyenlő szárú háromszög
- Derékszögű háromszög
- Általános háromszög
- Szabályos háromszög
Mely háromszögnek a kerületét számoljuk a következő képlettel: K = a + b + c
- Általános háromszög
- Egyenlő szárú háromszög
- Derékszögű háromszög
- Szabályos háromszög
Mely háromszögnek a kerületét számoljuk a következő képlettel: K = a + a + a
- Szabályos háromszög
- Általános háromszög
- Derékszögű háromszög
- Egyenlő szárú háromszög
Mely háromszögnek a kerületét számoljuk a következő képlettel: K = 3 · a
- Szabályos háromszög
- Általános háromszög
- Derékszögű háromszög
- Egyenlő szárú háromszög




